[7주차] 알고리즘

<백준 3830번>

https://www.acmicpc.net/problem/3830

3830번: 교수님은 기다리지 않는다

교수님은 기다리지 않는다 

 

문제

상근이는 매일 아침 실험실로 출근해서 샘플의 무게를 재는 일을 하고 있다. 상근이는 두 샘플을 고른 뒤, 저울을 이용해서 무게의 차이를 잰다.

교수님의 마음에 들기 위해서 매일 아침부터 무게를 재고 있지만, 가끔 교수님이 실험실에 들어와서 상근이에게 어떤 두 샘플의 무게의 차이를 물어보기도 한다. 이때, 상근이는 지금까지 잰 결과를 바탕으로 대답을 할 수도 있고, 못 할 수도 있다.

상근이는 결과를 출근한 첫 날부터 공책에 적어 두었다. 하지만, 엄청난 양의 무게가 적혀있기 때문에, 교수님의 질문에 재빨리 대답할 수가 없었다. 이런 상근이를 위해서 프로그램을 만들려고 한다.

상근이가 실험실에서 한 일이 순서대로 주어진다. 어떤 두 샘플의 무게의 차이를 구할 수 있는지 없는지를 알아내는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 이루어져 있다.

각 테스트 케이스의 첫째 줄에는 샘플의 종류의 개수 N (2 ≤ N ≤ 100,000)과 상근이가 실험실에서 한 일의 수 M (1 ≤ M ≤ 100,000)이 주어진다. 샘플은 1번부터 N번까지 번호가 매겨져 있다. 다음 M개 줄에는 상근이가 실험실에서 한 일이 주어진다.

상근이가 무게를 쟀다면, ! a b w와 같은 형식으로 주어진다. 이 뜻은 b가 a보다 w그램 무겁다는 뜻이다. (a ≠ b) w는 1,000,000을 넘지 않는 음이 아닌 정수이다. 모든 측정은 정확하고, 일관성을 유지한다.

교수님의 질문은 ? a b와 같은 형식으로 주어진다. 이 뜻은 b가 a보다 얼마나 무거운지를 출력하라는 뜻이다.

마지막 줄에는 0이 두 개 주어진다.

출력

교수님의 질문 (? a b)이 입력으로 들어올 때 마다, 지금까지 측정한 결과를 바탕으로 a와 b의 무게 차이를 계산할 수 있다면, b가 a보다 얼마나 무거운지를 출력한다. 무게의 차이의 절댓값이 1,000,000을 넘지 않는다. 만약, 측정한 결과를 바탕으로 무게의 차이를 계산할 수 없다면, "UNKNOWN"을 출력한다.

예제 입력 1 복사

2 2
! 1 2 1
? 1 2
2 2
! 1 2 1
? 2 1
4 7
! 1 2 100
? 2 3
! 2 3 100
? 2 3
? 1 3
! 4 3 150
? 4 1
0 0

예제 출력 1 복사

1
-1
UNKNOWN
100
200
-50

 

이 문제는 서로소 집합(자료구조)를 통해 풀 수 있다. 

1. 모든 노드에 대해서, 현재 노드의 값, 부모노드, 부모노드의 값을 저장

2. union의 경우 a,b,w가 주어질 때, (a-b)-w 만큼을 a에 대해서 갱신하고, a의 부모를 b의 부모에 포함시킨다.

3. 현재 부모노드와 현재 부모노드의 값을 미리 저장하고, 경로압축을 한 뒤 현재 부모노드의 값이 변했다면 그 변화량만큼을 현재 값에도 갱신

4. a,b의 부모가 같으면 차이를 출력, 다르면 unknown을 출력

 

class DisjointSet:
    def __init__(self, n):
        self.parent = list(range(n + 1))
        self.weight_diff = [0] * (n + 1)

    def find(self, x):
        if self.parent[x] == x:
            return x
        root = self.find(self.parent[x])
        self.weight_diff[x] += self.weight_diff[self.parent[x]]
        self.parent[x] = root
        return root

    def union(self, a, b, w):
        root_a = self.find(a)
        root_b = self.find(b)
        if root_a != root_b:
            self.parent[root_a] = root_b
            self.weight_diff[root_a] = self.weight_diff[b] - self.weight_diff[a] + w

def solve(test_cases):
    for n, m, actions in test_cases:
        ds = DisjointSet(n)
        for action in actions:
            if action[0] == '!':
                _, a, b, w = action.split()
                ds.union(int(a), int(b), int(w))
            elif action[0] == '?':
                _, a, b = action.split()
                root_a = ds.find(int(a))
                root_b = ds.find(int(b))
                if root_a == root_b:
                    print(ds.weight_diff[int(b)] - ds.weight_diff[int(a)])
                else:
                    print("UNKNOWN")

if __name__ == "__main__":
    test_cases = []
    while True:
        n, m = map(int, input().split())
        if n == 0 and m == 0:
            break
        actions = [input().strip() for _ in range(m)]
        test_cases.append((n, m, actions))

    solve(test_cases)

 

1. union(x, y, w): 이 함수는 x와 y를 합친다.
2. value[x]는 x가 속한 집합의 무게 차이를 나타내고, parentvalue[x]는 x의 부모 노드의 무게 차이를 나타낸다. 합칠 때, value[x]와 parentvalue[x]를 조정하여 각 노드가 속한 집합의 무게 차이를 업데이트한다.
3. findparent(x): 이 함수는 x의 부모 노드를 찾아 반환한다. 동시에 경로 압축과 함께 각 노드의 value와 parentvalue를 업데이트하여 각 노드의 무게 차이를 최신화한다.

주어진 입력에 대해 각각의 쿼리에 대한 처리를 수행하며, findparent 함수를 사용하여 각 노드의 부모를 찾고 무게 차이를 계산한다. 이 코드에서는 '?' 쿼리일 때 value[b] - value[a]를 출력하거나, 집합이 다르면 "UNKNOWN"을 출력한다. '!' 쿼리일 때는 union 함수를 호출하여 두 집합을 합친다. 경로 압축과 함께 Disjoint Set을 이용하여 각 쿼리에 대한 무게 차이를 효율적으로 계산하는 방식으로 문제를 해결한다.

 

 

 

 

 

 

 

 

<백준 2579번>

https://www.acmicpc.net/problem/2579

2579번: 계단 오르기

 

문제

계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

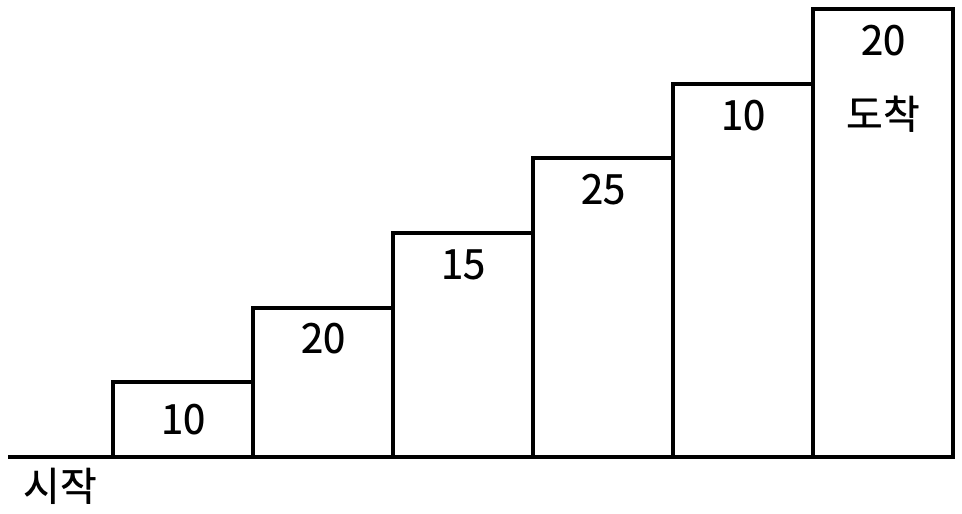
<그림 1>

예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

<그림 2>

계단 오르는 데는 다음과 같은 규칙이 있다.

1. 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
2. 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
3. 마지막 도착 계단은 반드시 밟아야 한다.

따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.

각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.

입력

입력의 첫째 줄에 계단의 개수가 주어진다.

둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.

출력

첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.

예제 입력 1 

6
10
20
15
25
10
20

예제 출력 1 

75

 

 

이 문제는 동적 계획법을 활용하여 풀 수 있다. 동적 계획법이란 하나의 큰 문제를 여러개로 나누어서 해결하는 것이고,

특정 데이터 내 최대화/최소화 계산을 해야할 때 주로 사용된다. 

 

def max_score(n, scores):
    if n == 1:
        return scores[0]
    elif n == 2:
        return scores[0] + scores[1]

    dp = [0] * n
    dp[0] = scores[0]
    dp[1] = scores[0] + scores[1]
    dp[2] = max(scores[0] + scores[2], scores[1] + scores[2])

    for i in range(3, n):
        dp[i] = max(dp[i-2] + scores[i], dp[i-3] + scores[i-1] + scores[i])

    return dp[-1]

if __name__ == "__main__":
    n = int(input())
    scores = [int(input()) for _ in range(n)]

    result = max_score(n, scores)
    print(result)

 

이 코드는 각 계단을 오를 때 최대 점수를 저장하는 리스트 dp를 활용한다. 3번째 계단부터는 이전 계단에서 올라오는 경우와 그 이전 계단에서 한 계단을 더 올라오는 경우 중 최댓값을 선택하면서 진행다. 결과적으로 마지막 계단까지 올라왔을 때의 최대 점수가 답이 된다.